Electric Circuits? It’s All About Nodes, Branches, and Loops

 

Nodes, Branches, and Loops

Since the elements of an electric circuit can be interconnected in several ways, we need to understand some basic concepts of network topology. To differentiate between a circuit and a network, we may regard a network as an interconnection of elements or devices, whereas a circuit is a network providing one or more closed paths.

The convention, when addressing network topology, is to use the word network rather than circuit. We do this even though the word network and circuit mean the same thing when used in this context.

In network topology, we study the properties relating to the placement of elements in the network and the geometric configuration of the network. It’s all about circuit elements such as branches, nodes, and loops.

Branches //

A branch represents a single element such as a voltage source or a resistor. In other words, a branch represents any two-terminal element.

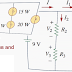
The circuit in Figure 1 has five branches, namely, the 10V voltage source, the 2A current source, and the three resistors.

Figure 1 – Nodes, branches, and loops

Nodes //

A node is the point of connection between two or more branches.

A node is usually indicated by a dot in a circuit. If a short circuit (a connecting wire) connects two nodes, the two nodes constitute a single node. The circuit in Figure 1 has three nodes a, b, and c.

Notice that the three points that form node b are connected by perfectly conducting wires and therefore constitute a single point. The same is true of the four points forming node c. We demonstrate that the circuit in Fig. 1 has only three nodes by redrawing the circuit in Fig. 2. The two circuits in Figs. 1 and 2 are identical.

However, for the sake of clarity, nodes b and c are spread out with perfect conductors as in Fig. 1.

Figure 2 – The three-node circuit of Figure 1 is redrawn

Loops //

A loop is any closed path in a circuit.

A loop is a closed path formed by starting at a node, passing through a set of nodes, and returning to the starting node without passing through any node more than once. A loop is said to be independent if it contains at least one branch which is not a part of any other independent loop. Independent loops or paths result in independent sets of equations.

It is possible to form an independent set of loops where one of the loops does not contain such a branch. In Fig. 2, abca with the 2Ω resistor is independent. A second loop with the 3Ω resistor and the current source is independent. The third loop could be the one with the 2Ω resistor in parallel with the 3Ω resistor. This does form an independent set of loops.

A network with b branches, n nodes, and l independent loops will satisfy the fundamental theorem of network topology //

b = l + n – 1

As the next two definitions show, circuit topology is of great value to the study of voltages and currents in an electric circuit.

Two or more elements are in series if they exclusively share a single node and consequently carry the same current.

Two or more elements are in parallel if they are connected to the same two nodes and consequently have the same voltage across them.

Elements are in series when they are chain-connected or connected sequentially, end to end. For example, two elements are in series if they share one common node and no other element is connected to that common node. Elements in parallel are connected to the same pair of terminals.

Elements may also be connected in a way that they are neither in series nor in parallel.

In the circuit shown in Fig. 1, the voltage source and the 5Ω resistor are in series because the same current will flow through them. The 2Ω resistor, the 3Ω resistor, and the current source are in parallel because they are connected to the same two nodes b and c and consequently have the same voltage across them. The 5Ω and 2Ω resistors are neither in series nor in parallel with each other.

 

Nodes, Branches, and Loops

Since the elements of an electric circuit can be interconnected in several ways, we need to understand some basic concepts of network topology. To differentiate between a circuit and a network, we may regard a network as an interconnection of elements or devices, whereas a circuit is a network providing one or more closed paths.

The convention, when addressing network topology, is to use the word network rather than circuit. We do this even though the word network and circuit mean the same thing when used in this context.

In network topology, we study the properties relating to the placement of elements in the network and the geometric configuration of the network. It’s all about circuit elements such as branches, nodes, and loops.

Branches //

A branch represents a single element such as a voltage source or a resistor. In other words, a branch represents any two-terminal element.

The circuit in Figure 1 has five branches, namely, the 10V voltage source, the 2A current source, and the three resistors.

Figure 1 – Nodes, branches, and loops

Nodes //

A node is the point of connection between two or more branches.

A node is usually indicated by a dot in a circuit. If a short circuit (a connecting wire) connects two nodes, the two nodes constitute a single node. The circuit in Figure 1 has three nodes a, b, and c.

Notice that the three points that form node b are connected by perfectly conducting wires and therefore constitute a single point. The same is true of the four points forming node c. We demonstrate that the circuit in Fig. 1 has only three nodes by redrawing the circuit in Fig. 2. The two circuits in Figs. 1 and 2 are identical.

However, for the sake of clarity, nodes b and c are spread out with perfect conductors as in Fig. 1.

Figure 2 – The three-node circuit of Figure 1 is redrawn

Loops //

A loop is any closed path in a circuit.

A loop is a closed path formed by starting at a node, passing through a set of nodes, and returning to the starting node without passing through any node more than once. A loop is said to be independent if it contains at least one branch which is not a part of any other independent loop. Independent loops or paths result in independent sets of equations.

It is possible to form an independent set of loops where one of the loops does not contain such a branch. In Fig. 2, abca with the 2Ω resistor is independent. A second loop with the 3Ω resistor and the current source is independent. The third loop could be the one with the 2Ω resistor in parallel with the 3Ω resistor. This does form an independent set of loops.

A network with b branches, n nodes, and l independent loops will satisfy the fundamental theorem of network topology //

b = l + n – 1

As the next two definitions show, circuit topology is of great value to the study of voltages and currents in an electric circuit.

Two or more elements are in series if they exclusively share a single node and consequently carry the same current.

Two or more elements are in parallel if they are connected to the same two nodes and consequently have the same voltage across them.

Elements are in series when they are chain-connected or connected sequentially, end to end. For example, two elements are in series if they share one common node and no other element is connected to that common node. Elements in parallel are connected to the same pair of terminals.

Elements may also be connected in a way that they are neither in series nor in parallel.

In the circuit shown in Fig. 1, the voltage source and the 5Ω resistor are in series because the same current will flow through them. The 2Ω resistor, the 3Ω resistor, and the current source are in parallel because they are connected to the same two nodes b and c and consequently have the same voltage across them. The 5Ω and 2Ω resistors are neither in series nor in parallel with each other.